Activation Function에서 활용한 sigmoid와 Softmax가 어떤 역할을 하는 지 배워보자.
sigmoid와 softmax는 어떤 차이가 있는지, 각각 어떻게 활용되는지 확인해보자.
sigmoid는 왜 탄생되었을까라는 생각도 해볼 수 있다.
Sigmoid Function
sigmoid를 알기 전에 Logit을 알아야하고, Logit을 알기 전에 odds 를 알아야한다.
그 이유는 sigmoid는 odds에서 변형되어, 탄생됐기 때문이다.
Odds ratio
odds ratio는, 한 사건이 일어날 확률 대비 한 사건이 일어나지 않을 확률의 비율?이라고 생각하면 된다.
예를 들어,
동전을 던질 때, 뒷면이 나올 확률 대비 앞면이 나올 확률은 1이다. 두 확률이 동일하기 때문이다.
odds 식은 O = P/1-P 다.
odds ratio는 아래와 같은 그래프를 형성한다. (확률이 1에 가까워 질수록 양의 무한이 되는 것을 볼 수 있다.)

Logit 함수
Logit 함수는 odds에 log를 씌운 것이다.
odds의 다른 표현이라고 생각하면 된다. odds에 log를 씌운 이유는 연산하기 수월해지기 때문이다.
logit 함수의 식은 Logit = log(p/1-p) 다.
logit 함수의 특징은 확률 0.5를 기준으로 logit 값이 음수와 양수로 나뉜다.
logit 함수의 그래프는 아래와 같다.(확률이 0에 가까워 질수록, 음의 무한이 / 1에 가까워 질수록, 양의 무한이 된다.)

Sigmoid 함수
sigmoid 함수는 logit 함수를 "p =" 형태로 변형시킨 것이다.
즉, 값이 확률을 의미하도록 변형시킨 식이라고 생각하면 된다.

logit 값을 확률로 변형시킨 이유는
Binary Classifiers에서 마지막 결과가 확률의 의미를 가지는 값이 나와야하기 때문이다. (&두 분류로 나눠야하기 때문.)
sigmoid 그래프 결과는 아래와 같다.(Logit값이 음의 무한으로 가면, sigmoid값은 0에 수렴하고, Logit값이 양의 무한으로 가면, sigmoid값은 1에 수렴한다.)

※딥러닝에서는 Affine Function을 거쳐 나온 Z값을 Logit 값으로 생각하여 activation Function중 sigmoid에 넣어 나온 P인 확률값을 최대한 실제 확률값으로 만드는 것이 목표다.
이제 Logit 값과 Sigmoid 값이 어떻게 Layers에서 활용되는지 알아보자.
아래는 sigmoid activation Function을 활용한 일반적인 Dense Layers를 구성한 것이다.

위 과정은 마지막 layer에 Sigmoid activation Function을 실행할 Neuron을 하나 추가하여 마지막 Output이 확률값이 되도록 한다.
Binary Classification을 위한 Output을 만들어준 것이다.
Binary Classification이란 2개의 범주형 데이터를 활용한 분류를 말한다.
또한, 위 과정의 러닝을 Logistic Regression이라 한다.
Logistic Regression
독립 변수의 선형결합(affine Function)으로 종속변수를 설명하는 선형회귀와 비슷하지만, 종속변수가 범주형 데이터를 대상으로 하여 일종의 분류 기법으로도 볼 수 있다.
회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도학습 알고리즘이다.
머신러닝에서 Binary Classification 모델로 사용되는 것이 로지스틱 회귀 알고리즘이다.
Softmax Layer
softmax layer는 다양한 class를 분류하여 확률을 계산할 때, 사용한다.
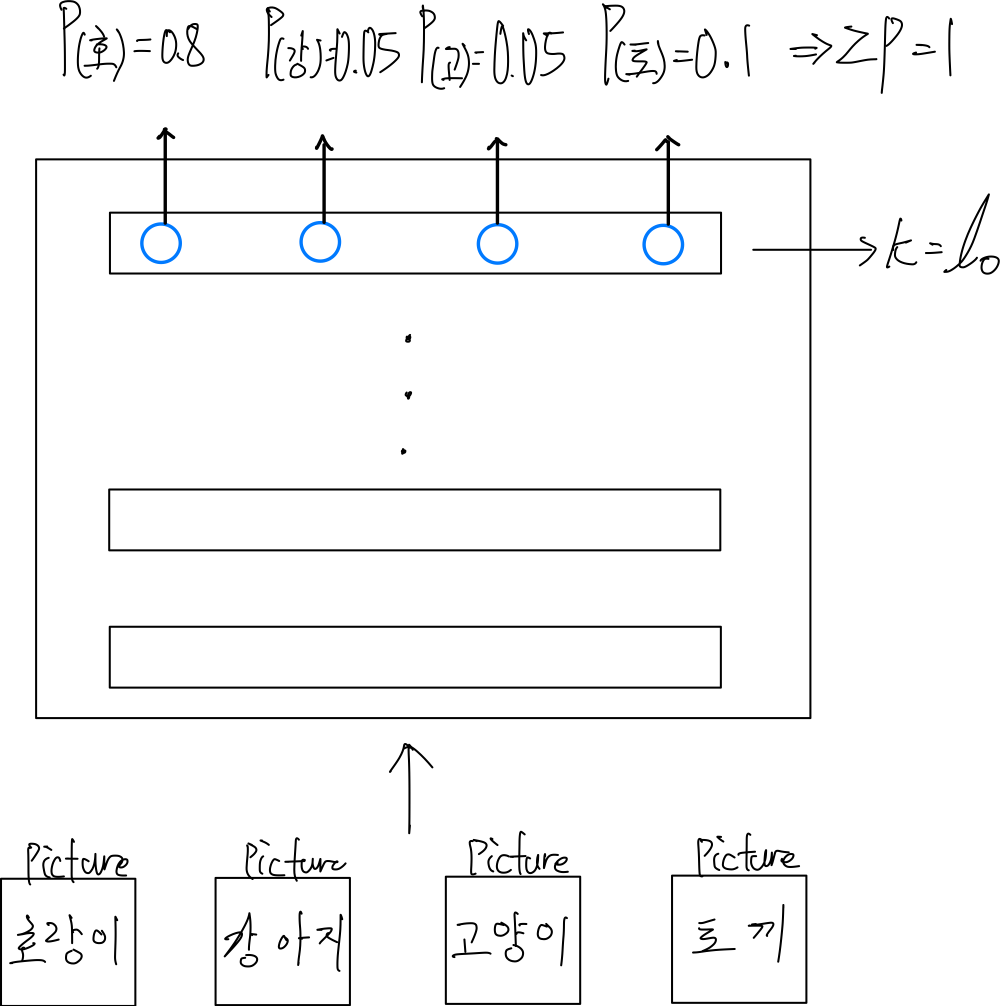
위 그림과 같이 한번에 다양한 데이터를 입력하여, 각 데이터에 대한 확률값을 도출해내야할 때, 사용된다.
각 데이터에 관하여, 도출된 확률값들의 합은 무조건 1이 되어야한다.(당연한 말이기도 하다.)
softmax layer의 neuron network 구성을 알아보자.
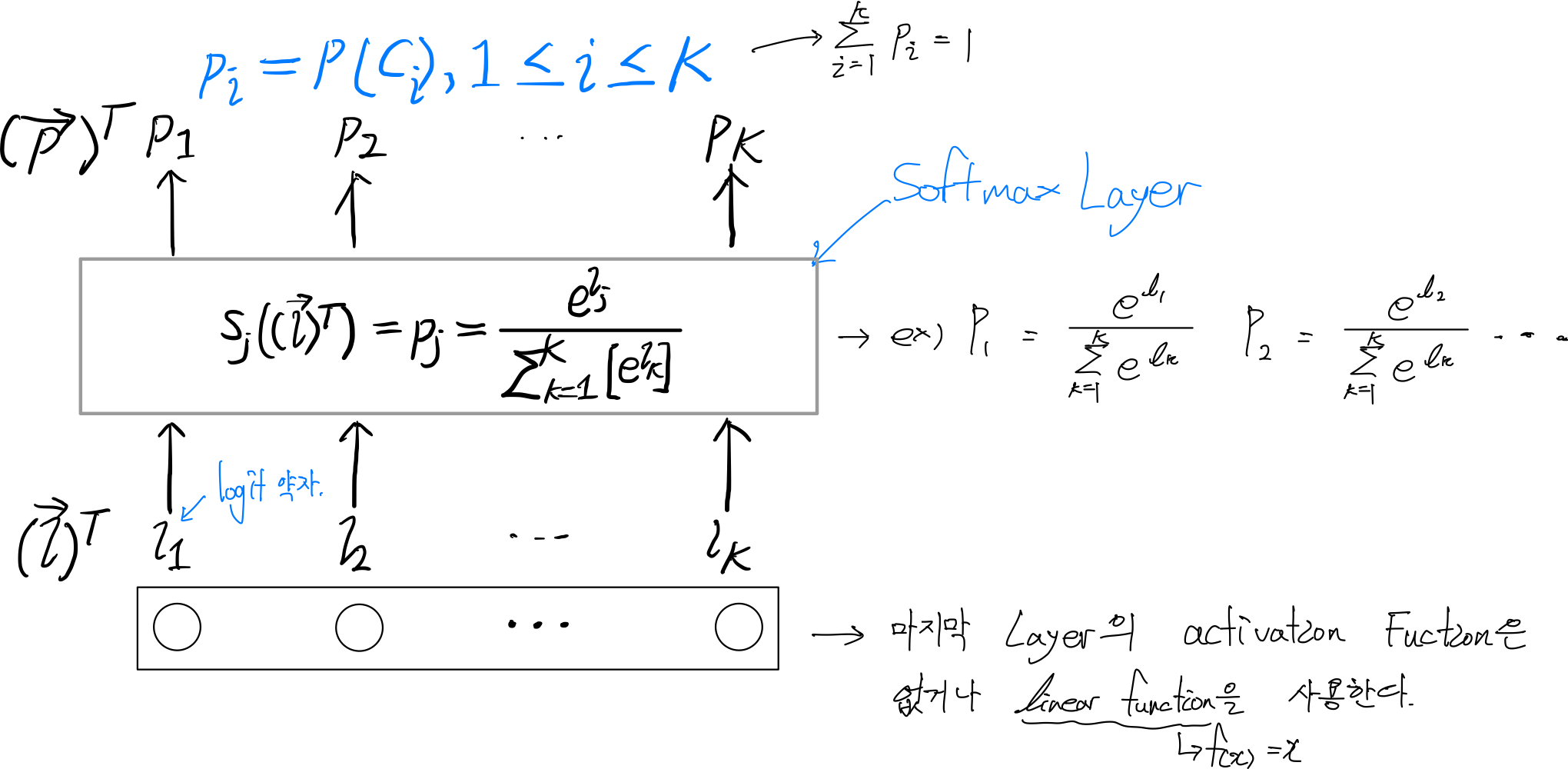
Softmax Layer의 특징
- Softmax 이전 layer에는 activation Function을 사용하지 않거나, linear Function을 사용한다.
그 이유는 softmax 역할을 하는 layer가 이 후에 나와서, activation Function과 같은 역할을 해야하기 때문이다.
- 다양한 분류가 필요할 때, 사용된다.
- Softmax 이전 layer의 neuron 개수는 logit 값의 개수와 동일하고, softmax layer의 출력값인 provability의 개수와 동일하다.
입력 데이터의 크기가 (N X ℓ0-1)으로 들어온다면, softmax 이전 layer에서는 neuron개수(ℓ0)로 인해 (N X ℓ0)가 될 것이고, softmax layer에서는 이에 맞는 softmax 개수가 나오므로, (N X ℓ0)크기의 provability 개수가 나올 것이다.
Softmax 와 Sigmoid의 차이점
Softmax Layers와 Sigmoid의 Neuron Network 구성에서의 차이점은 아래와 같다.

- Softmax 는 하나의 layer가 softmax의 역할을 하고 Sigmoid는 하나의 layer에서 Affine Function을 거친 Activation Function중 하나의 함수다.
- Softmax는 이전 layer에서 logit값을 받고 Sigmoid는 현재 layer 속에서 Affine Function을 거친 값을 logit으로 한다.
- Softmax는 logit vector를 받아서 provability vector를 추출하고, Sigmoid는 logit 1개를 받아서 provability 1개를 추출한다.
마무리
이미지인식, 컴퓨터 비전에서 가장많이 사용되고 있는 이론을 배워봄으로써, 설렘은 한층더 올라갔다. 빨리 많은 것들을 배워서 이런 이론들을 응용하여, 의미있는 곳에 사용해보고 싶다. 그렇게 하기 위해서는 insight도 길러야함을 잘 알기때문에, 꼭 책도 틈틈이 자주 읽자.
'Data_study > Deep Learning' 카테고리의 다른 글
| [Deep_learning] Multiclass_Classifiers 구현 (0) | 2022.07.12 |
|---|---|
| [Deep_learning] Binary Classifiers 구현 (0) | 2022.02.23 |
| [Deep_learning] Dense Layers 구현 (0) | 2022.02.04 |
| [Deep Learning] Dense Layers 이론 (0) | 2022.01.30 |
| [Deep_learning] Artificial Neurons 구현 (0) | 2022.01.18 |