Dense Layers를 설명하기 앞서, Layers가 무엇인지 설명하겠다.
Layer란, 음향 장비중에 믹서에서 이퀄라이저와 비슷한 역할을 한다. 이퀄라이저도 하나의 음성이 들어오면, 각각의 High, mid, low의 기존에 입력된 parameter들을 통해, layer들을 통과하여, 변형된 음성을 출력한다.
이와같이 layer도 동일하다. 데이터 세트 X를 입력하면, 각 neuron들의 parameter를 통해 새로운 결괏값을 도출해낸다.
이 부분도 데이터세트와 뉴런, 결괏값들의 차원이 중요하다.
Dense Layers
Layer는 서로 다른 Parameter(Weight, Bias)들을 가지고 있는 Parametric Function들의 모임이다.
즉, 저번 개시글에서 배운 Neuron들의 집합이라고 생각면된다. 다양한 Neuron들이 하나의 층을 형성하고 그것을 layer라고 부른다.
그리고, Dense Layers는 모든 입력값(x1,x2,x3,x4,xli)가 각각의 뉴런에 모두 들어가는 것을 말한다.

- vector 차원에서의 Dense Layers에 속해있는 파라미터들을 확인해보자.
각 파라미터들의 차원들을 유심히 봐보자.

- -Input vector (vector X transposed)가 ℓI(엘아이)개 있기 때문에 Weight(vector W)도 ℓI개 있어야한다.
그 이유는 행렬곱의 개념을 가져와 실행하기 때문인데, 행렬곱은 XY인 경우에 X의 열의 개수와 Y의 행의 개수가 같아야 각 원소끼리 곱하면서 더해져가기 때문이다.
- -Neuron이 ℓ1개 있으면 weight 자체, bias 자체도 ℓ1개 있다.
그 이유는 각 neuron에 각 weight와 bias가 할당되어 있을 거기 때문이다. 이부분이 하나의 layer에서는 당연한 말이라고 생각되겠지만, 층이 깊어질 수록 헷갈려질 수 있다. 유의해놓자.
-선형대수학의 개념을 활용하여, 흩어져있는 Weight(vector)를 Weight(Metrix)로, bias(원소)를 bias(vector)로 묶어서 한번에 계산해보자.

각 neuron에 있었던 Weight들을 하나의 metrix로 만들고, bias들은 하나의 vector로 만들어서 한번에 연산을 진행하는 것이다.
- -Input 값 X의 열 개수와는 관계없이 결괏값 a vector는 neuron의 개수 ℓ1과 연관된 vector (1,ℓ1) 형태다.
이유는 X ∈ R(1xℓI) 가 들어오면, 우선 W(metrix) ∈ R(ℓIxℓ1)와 행렬곱을 실행하여, bias(vector transposed) ∈ R(1xℓ1)와 더해주면, (1 x ℓI) * (ℓI x ℓ1) + (1 x ℓ1) = (1 x ℓ1)로 결괏값 a vector는 shape = (1 , ℓ1)가 된다.
- - 결괏값 a는 X * W + b 의 결괏값 Z에 activation function인 g( ) 을 진행해줘서 나온 값이다.
Generalized Dense Layers
이제는 하나의 layer가 아닌 겹겹이 층으로 이루어진 layer를 다루어보자.
입력데이터를 먼저 맞이한 layer를 통과한 결괏값은 그 다음 layer의 입력값으로 들어가서 연산이 진행되는 식이다.
-두개의 layer가 순차적으로 어떻게 연산이 되고 입력데이터는 어떤 과정을 통해 결괏값이 도출되는지 확인해보자.

- -각 layer별 파라미터 개수는 ℓI (Input data X의 행 개수) x ℓ1(현재 layer의 neuron 개수) + 1 x ℓ1(현재 layer의 neuron 개수)다.
- -이전 layer의 결괏값 a1이 다음 layer의 입력값으로 들어가고 이에 맞게 weight와 bias 개수가 할당 되어 연산된다.
-가장 일반적인 i개의 layer들이 어떻게 진행되는지 확인해보겠다.

- -각 layer별 파라미터 개수는 ℓi-1 (이전 layer 결괏값의 행개수) x ℓi(현재 layer의 neuron 개수) + 1 x ℓi(현재 layer의 neuron 개수)다.
Minibatch in Dense Layers
minibatch는 대량의 데이터 세트를 분할하여 분석을 진행하는 것이다. 이렇게 대량의 데이터를 분할하여 layer에 넣는 이유는 큰 데이터를 한번에 다루기 위해서는 그에 맞는 하드웨어가 필요한데, 이렇게 되면 비용적인 문제가 있기 때문이다.
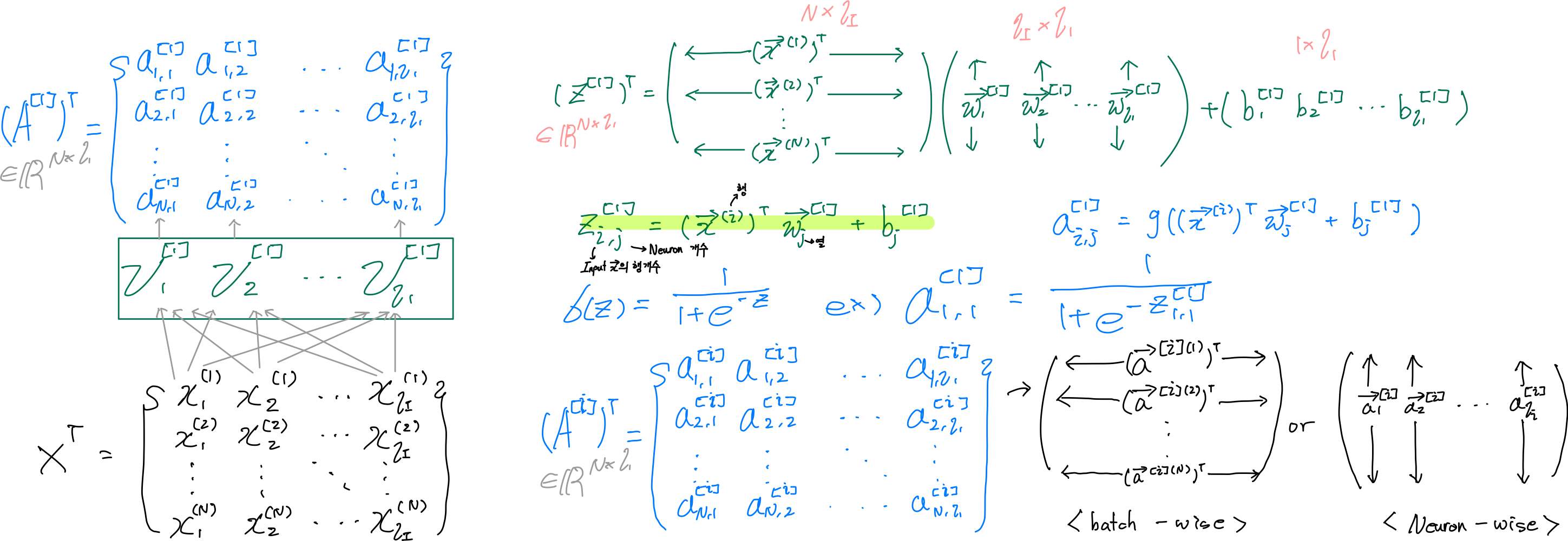
- -기본 Dense Layers와 다른 점은 입력 데이터의 행개수가 1이 아닌 N개다. 그로 인해, 결괏값 a도 N x ℓi로 바뀐다.
- -데이터 세트가 많아진다고 해도, Weight와 bias의 차원에는 영향을 주지 않는다.
그 이유는 어차피 입력데이터 X 행의 개수가 많아진다고 해도, Weight와 bias간의 연산에서는 X 하나의 행과 Weight가 행렬곱 연산이 진행되기 때문이다.
- -affine Function의 결괏값인 Z(i x j)에서 i는 Input X의 행 개수, j는 Neuron 개수다.
Cascaded Dense Layers
이번에는 층층이 쌓인 layers의 표본을 공부해보자. (이부분도 마찬가지로, 각 파라미터와 입력데이터, 결괏값들의 shape들을 주시하자.)

입력된 X(Transposed)가 어떤 크기의 weight와 bias들로 변형되는지 확인해보자.
- -마지막 layer를 통과한 결괏값 A는 (입력된 X의 행개수,마지막 layer의 neuron개수)의 shape를 형성한다.
이유는 어차피 weight와 bias값은 입력된 set의 열개수에 맞게 할당되어 행렬곱 연산을 진행하고 마지막 layer의 neuron개수에 의해, weight와 bias 개수가 정해지기 때문이다.
마무리
모든 발명과 개발은 주변에 있는 당연함으로 지나갔던 것들을 응용하여 만들어지는 구나를 다시한번 느꼈다. datascientist의 중요한 덕목중 하나인 융합적 사고력과 통찰력을 기르도록 독서를 많이 해서 길러보자.
하나하나 배워가는데, 즐거움이 존재함을 처음으로 data분야에서 느꼈다. 그냥 넘어가는 것 없이 꼼꼼히 공부하자.
'Data_study > Deep Learning' 카테고리의 다른 글
| [Deep_learning] Binary Classifiers 구현 (0) | 2022.02.23 |
|---|---|
| [Deep Learning] Sigmoid and Softmax 이론 (0) | 2022.02.18 |
| [Deep_learning] Dense Layers 구현 (0) | 2022.02.04 |
| [Deep_learning] Artificial Neurons 구현 (0) | 2022.01.18 |
| [Deep Learning] Artificial Neurons 이론 (0) | 2022.01.16 |