Purpose : housing data로 미국 서구의 집값을 예측하자.
Import data
우선 필요한 패키지들을 불러오고, 데이터가 있는 링크를 하나의 객체로 설정해둔다.
import os
import tarfile
import urllib
import pandas as pd
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/"
HOUSING_PATH = os.path.join("datasets","housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"Data 불러오기
fetch_housing_data는 데이터를 추출하는 함수(데이터를 내려받는 일을 자동화 시키는 함수)
한번 함수로 구성해두면 자주 사용할 수 있으니, 우선 만들어보았다.
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
os.makedirs(housing_path,exist_ok=True)
#os.makedirs()함수를 활용하여 local path에 해당하는 폴더 만들기
tgz_path = os.path.join(housing_path, "housing.tgz")
#os.path.join()는 두 문자열을 결합할때 사용, 파일 변환에 사용, 각 문자열 사이에 /가 들어가면서 결합된다.
urllib.request.urlretrieve(housing_url,tgz_path)
#urllib.request.urlretrieve()는 파일을 다운로드할때 사용
#아래 코드는 압축해제하는 과정
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()아래 코드는 위 함수로 내려받은 데이터를 불러오는 함수를 생성한 것이다.
def load_housing_data(housing_path=HOUSING_PATH):
#os.path.join()는 파일 변환에 사용
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
Data 탐색
함수들을 실행시키고 데이터를 확인해보자.
fetch_housing_data()
housing = load_housing_data()
housing.head()
housing.describe()
housing.info() #데이터 속성들이 어떤 type인지와 데이터의 유형과 규모를 확인해보자.

ocean_proximity 속성이 object type임을 알 수 있다.
어떤 카테고리가 있는지 확인해보자.
housing["ocean_proximity"].value_counts()
#value_counts()는 어떤 카테고리가 있고 각 카테고리마다 얼마나 많은 구역이 있는지 확인할때 사용
Train Data & Test Data
데이터 세트를 분석하여 성과를 확인하기 위해 훈련세트와 테스트세트로 나누자.
import numpy as np
def split_train_test(data,test_ratio): #변수는 data파일과 훈련*테스트데이터의 비율이다.
shuffled_indices = np.random.permutation(len(data)) #무작위로 섞인 배열을 만듦.
test_set_size = int(len(data)*test_ratio)#data의 길이에 비율을 곱하여 숫자형태로 만듦.
test_indices = shuffled_indices[:test_set_size] #위 숫자 순번까지 test데이터를
train_indices = shuffled_indices[test_set_size:]#위 숫자 순번부터 끝까지 train데이터로 만듦.
return data.iloc[train_indices],data.iloc[test_indices]
#iloc매소드는 [행,열]로 순번을 입력하여 데이터를 추출할 수 있다.
#loc매소드도 있는데 이건 행과 열의 이름나 조건표현으로 추출할 수있다.
train_set, test_set = split_train_test(housing,(0.2))
print(len(train_set))
print(len(test_set))
하지만, 이 방법은 괜찮지만 완벽하지 않다. 함수를 다시 실행하면 또 다른 세트가 추출되기 때문에 여러번 계속하면 우리는 전체 데이터셋을 보는 셈이 된다. np.random.seed()으로 초깃값을 지정한다고 해도 업데이트된 데이터셋을 사용하게되면 문제가 생긴다.
위 문제를 해결하기 위해서는, 각 데이터에 식별자를 사용하여 테스트 세트로 보낼지 말지 결정을 하는 방법을 사용하면된다. 이렇게 하면 여러번 반복 실행되면서 데이터셋이 갱신되더라도 테스트 세트는 동일하게 유지된다.
#crc란, 파일또는 문자의 고유한 지문에 해당하는 것
from zlib import crc32
def test_set_check(identifier, test_ratio):
return crc32(np.int64(identifier)) & 0xffffffff < test_ratio *2 **32
def split_train_test_by_id(data,ratio,id_column):
ids = data[id_column]
in_test_set = ids.apply(lambda id_:test_set_check(id_,test_ratio))
return data.loc[~in_test_set],data.loc[in_test_set]
housing_with_id = housing.reset_index()
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")
안타깝게도 주택 데이터셋에는 식별자 컬럼이 없어서 행의 인덱스를 ID로 사용했다. 하지만, 행의 인덱스를 고유 식별자로 사용할 때 새데이터는 데이터셋의 끝에 추가되어야 하고 어떤 행도 삭제되지 않아야한다.
이것이 불가능할 경우 고유 식별자를 만드는데 안전한 특성을 사용해야한다. 예를 들어 경도'위도와 같은 고유 특성등등..
housing데이터에서는 경도와 위도로 고유 식별자를 만들었다.
housing_with_id["id"]= housing["longitude"] *1000 + housing["latitude"]
train_set, test_set = split_train_test_by_id(housing_with_id,0.2,"id")위와 같이 직접함수를 만들어서 세트를 나눠도 좋지만 한계는 존재한다.
사이킷런은 데이터셋을 여러 서브셋으로 나누는 다양한 방법을 제공한다.
가장 간단한 함수는 train_test_split인데 위에 함수로 만든 {split_train_test}와 비슷하지만 두가지 특징이 더있다.
첫째, 난수 초깃값을 지정할 수 있는 random_state 매개변수가 있다.
둘째, 행의 개수가 같은 여러개의 다른 데이터 셋을 넘겨서 같은 인덱스를 기반으로 나눌수있다
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing,test_size=0.2,random_state=42)
하지만, 위와 같은 무작위 샘플링 방식은 데이터셋이 충분히 크다면 일반적으로는 괜찮지만, 그렇지 않다면 샘플링 편향이 생길 수 있다.
그러므로 계층적 비율을 유지하며, 세트를 구성해야한다.(=계층적 샘플링)
housing["income_cat"] = pd.cut(housing["median_income"], #pd.cut 함수를 사용해 카테고리 5개를 가진 소득 카테고리 특성을 만든다.
bins=[0,1.5,3.0,4.5,6.,np.inf], #np.inf는 무한이라는 의미.
labels=[1,2,3,4,5])
StratifiedShuffleSplit는 계층샘플링과 랜덤 샘플링을 합친 것,모집단을 여러개의 층으로 구분하여, 각 층에서 n개씩 랜덤하게 추출하는 방법이다.(stratified가 붙으면 계층형 샘플링임을 인지하면 된다.)
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
#n_splits는 분리할 데이터 셋의 개수를 지정, test_size는 테스트 셋의 비율을 지정, random_state는 난수를 지정
for train_index, test_index in split.split(housing, housing["income_cat"]): #split(datframe,대상) : 데이터프레임을 대상을 기준으로 나눈다.
strat_train_set= housing.loc[train_index]
strat_test_set = housing.loc[test_index]위에서의 split 객체를 사용할때는 좀더 복잡한 그룹을 사용한다거나, 다양한 경우를 위해서 사용한다.
보통은 아래와 같이 train_test_split로도 구동 가능하다.
st_train_set, st_test_set = train_test_split(housing, test_size= 0.2,random_state=42,stratify=housing["income_cat"])
strat_test_set["income_cat"].value_counts()/len(strat_test_set) #각 카테고리에 속한 value들을 센 후, data set의 크기로 나눈 것.
housing["income_cat"].value_counts() / len(housing) #stratified로 나눈것과 실제 데이터에서의 비율이 같음을 알 수 있다.위 두줄을 실행하면 각 계층마다 동일한 비율로 샘플링되었음을 알 수 있다.
그럼 이제 random 샘플링이 어느정도 오차가 있는지와 startified 샘플링이 어느정도 오차가 있는지를 확인해보자.
def income_cat_proportions(data):
return data["income_cat"].value_counts() / len(data) #각 레이블의 데이터 비율을 계산하는 함수 생성
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
compare_props = pd.DataFrame({
"Overall": income_cat_proportions(housing),
"Stratified": income_cat_proportions(strat_test_set),
"Random": income_cat_proportions(test_set),
}).sort_index(ascending=False) #dataFrame을 형성함. overall/stratified/random으로 행렬 구성 sort_index()는 오름차순 내림차순을 관여함.
#sort_index(ascending=False)는 내림차순이고 ()이렇게 비워놓으면 기본값 오름차순이 된다.
compare_props["Rand. %error"] = 100 * compare_props["Random"] / compare_props["Overall"] - 100
compare_props["Strat. %error"] = 100 * compare_props["Stratified"] / compare_props["Overall"] - 100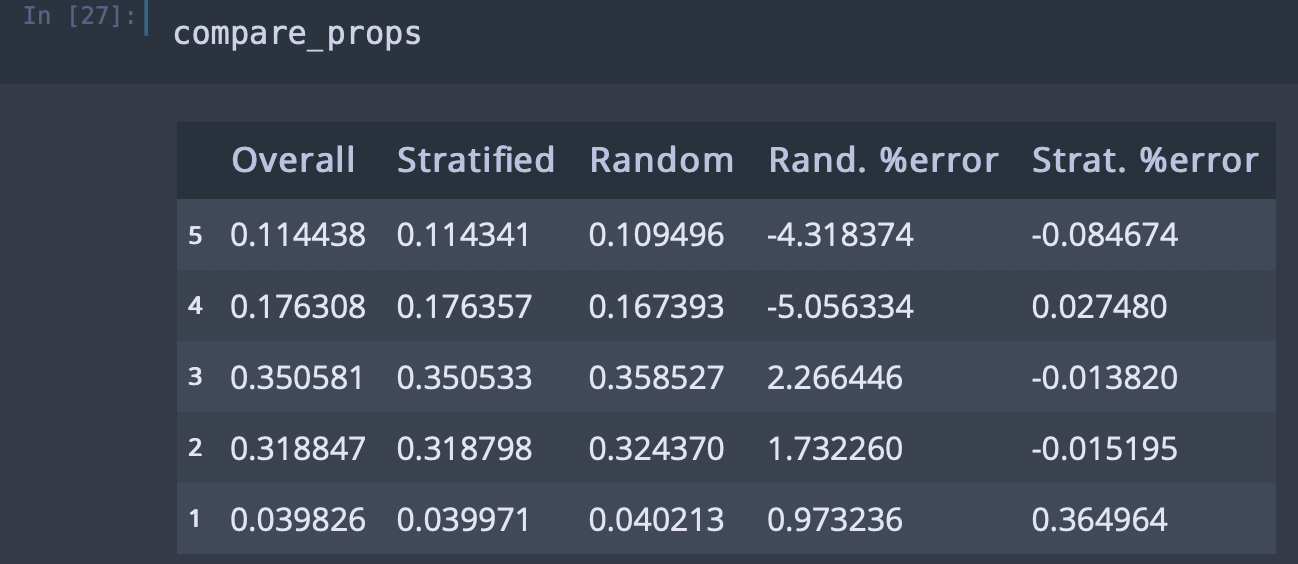
이제 testset과 trainset을 나눴으니 income_cat의 항목은 필요없으므로 삭제해서 데이터를 원래 상태로 되돌린다.
for set_ in (strat_train_set,strat_test_set):
set_.drop("income_cat", axis=1,inplace=True)
#inplace = True는 호출된 데이터프레임 자체를 수정하고 아무런 값도 반환하지 않는다.
housing= strat_train_set.copy() #기존 데이터에 손상이 가지않도록 복사본을 만들어 사용한다.
Data 시각화
데이터를 시각화하여, 지도를 통해 데이터를 확인해보자.
housing.plot(kind="scatter",x="longitude",y="latitude",alpha =0.4,
s=housing["population"]/100,label = "population",figsize=(10,7), #s는 원의 크기를 말한다.
c="median_house_value",cmap=plt.get_cmap("jet"),colorbar=True,
#c는 컬러를 선택하는 옵션이다. 거기에 데이터가 들어가면 데이터의 크기만큼 색을 관여한다. cmap(컬러)는 어떤 색의 유형을 선택할 것인지.를 관여한다.
#jet 컬러맵는 색깔의 유형중 하나다. 데이터가 높으면 빨간색, 낮으면 파란색
sharex=False
#sharex=False는 판다스의 버그인데, 이것을 주지않으면, x축이 나타나지 않는다.
)
plt.legend()
위 그림은 LA 지도를 알고 있어야 해석이 가능하다. 그래서 이 그래프에 지도를 한번 첨가해보자.
우선, LA 지도 이미지 파일을 내 컴퓨터에 저장하고 불러온다.
# 그림을 저장할 위치
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "end_to_end_project"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
# ./images/end_to_end_project로 현재 작업중인 곳에 디렉토리를 생성했다.
#save_fig 함수 생성
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("그림 저장:", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# California image 다운로드
PROJECT_ROOT_DIR = "."
images_path = os.path.join(PROJECT_ROOT_DIR, "images", "end_to_end_project")
os.makedirs(images_path, exist_ok=True)
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/"
filename = "california.png"
print("Downloading", filename)
url = DOWNLOAD_ROOT + "images/end_to_end_project/" + filename
urllib.request.urlretrieve(url, os.path.join(images_path, filename))
이제 다운로드해온 사진을 matplotlib.image 모듈을 활용해서 이미지를 첨가해보자.
#california 지도 사진에 plot분석그림 겹쳐 넣기
import matplotlib.image as mpimg
california_img=mpimg.imread(os.path.join(images_path, filename))
#matplotlib.image 모듈을 활용해서 imread()메소드를 사용하여 현재 작업 디렉토리에서 사진을 불러온다.
ax = housing.plot(kind="scatter", x="longitude", y="latitude", figsize=(10,7),
s=housing['population']/100, label="Population",
c="median_house_value", cmap=plt.get_cmap("jet"),
colorbar=False, alpha=0.4)
#위에서는 일단 데이터를 시각화한 그래프를 불러온것. colorbar를 False로 놓은 것은 밑에서 따로 만들려고 함이다.
plt.imshow(california_img, extent=[-124.55, -113.80, 32.45, 42.05], alpha=0.5,
cmap=plt.get_cmap("jet"))
#불러온 california_img에서 범위(extent)를 정하고 투명도(alpha)도 정한다
plt.ylabel("Latitude", fontsize=14)
plt.xlabel("Longitude", fontsize=14)
prices = housing["median_house_value"]
tick_values = np.linspace(prices.min(), prices.max(), 11)
#np.linspace는 같은간격으로 (start,stop,num) start에서 stop까지 num 갯수로 나누는것.
cbar = plt.colorbar(ticks=tick_values/prices.max())
cbar.ax.set_yticklabels(["$%dk"%(round(v/1000)) for v in tick_values], fontsize=14) #round()함수는 반올림하여 정수로 만듦.
cbar.set_label('Median House Value', fontsize=16)
plt.legend(fontsize=16)
save_fig("california_housing_prices_plot")
plt.show()
이렇게 이미지를 첨가하여 시각화된 데이터를 보니, 더 구체적으로 데이터를 분석할 수 있다.
해변쪽에 있는 집이 더 높은 가격대로 형성되어 있다는 사실도 알 수 있는등 매우 보기 편하다.
상관관계 조사
#표준 상관계수(피어슨의 r)를 메스드를 이용해 계산한 것임.
corr_matrix = housing.corr()
housing.corr()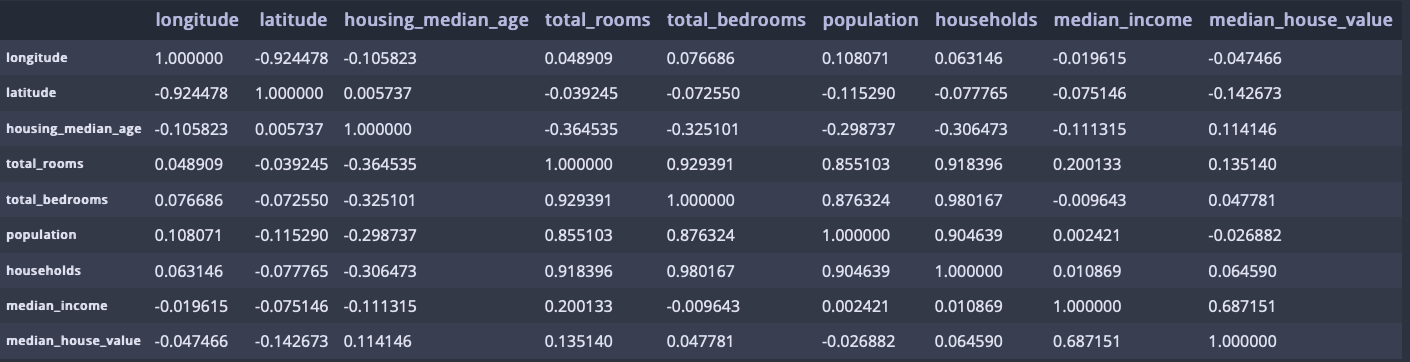
우린 집값을 예측하는 것이므로 median_housing_value 속성과 나머지의 속성간의 상관관계를 분석해보자.
아래 결과를 통해, median_house_value는 median_income와 가장 높은 양의 상관관계임을 알 수 있다.
corr_matrix["median_house_value"].sort_values(ascending=False)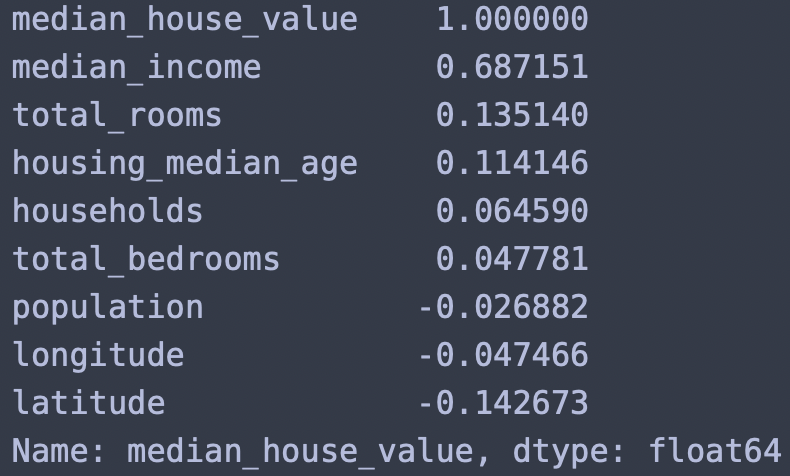
가장 높게 나온 median_income과 median_house_value의 상관관계를 plot함수를 통해 그래프로 확인해보자.
housing.plot(kind="scatter",x="median_income",y="median_house_value",alpha=0.5)
위 그래프를 통해 median_income과 median_house_value는 양의 상관관계가 매우 강함을 알 수 있고, $500000에서 수평선을 보임을 알 수 있다. 그리고, $450000,$350000와 $280000에서도 수평선이 있음을 볼 수 있다. 수평선을 그리는 구간의 데이터는 알고리즘이 이런 이상한 형태를 학습하지 않도록 해당 구역을 제거하는 것이 좋다.
median_income에 영향을 줄 법한 특성을 만들어보자. 나는 아래와 같이 세개를 만들어봤고 median_house_value와의 상관성을 분석해보았다.
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"] = housing["population"]/housing["households"]
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)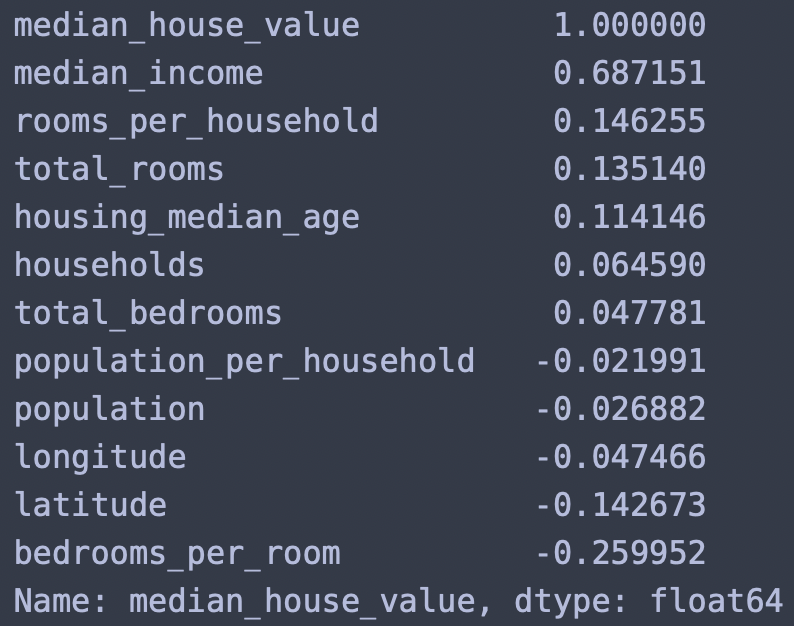
큰 수치의 값들을 만들어내지는 못했지만, bedrooms_per_room과 rooms_per_household는 유심히 봐볼 필요가 있어보인다.
지금까지는 데이터를 수집하고 그래프를 그려 살펴보고 상관관계도 수치로 알아보았다. 지금부터는 모델링을 하기 좋게 전처리할 것이다.
Data 전처리 - 데이터 정체
이제 분석에 들어가기전 분석하기 좋은 데이터 상태를 만들어 놓는 단계다.
먼저, 훈련을 할 세트인, train_set에 있는 median_house_value 레이블을 삭제하고 시작하자.(훈련을 하는데 정답이 있으면 안되므로..)
housing = strat_train_set.drop("median_house_value",axis=1)
housing_labels = strat_train_set["median_house_value"].copy()
이제 분석을 위해 데이터 속에 누락된 값인 null값이 있는지 확인해보자.
sample_incomplete_rows = housing[housing.isnull().any(axis=1)] #any는 조건중 하나라도 맞으면 true, all은 조건이 다맞아야 true
sample_incomplete_rows위 코드 결과, total_bedrooms 레이블에 null값이 많음을 알 수 있다.
null 값을 해결하는 방법은 세가지가 있다.
옵션 1.해당 구역을 제거한다/ 옵션2. 전체 특성을 삭제한다./ 옵션3. [0또는 평균값, 중간값...]와 같은 값으로 채운다.
sample_incomplete_rows.dropna(axis=1) #옵션1 na가 있다면 열(axis=1)를 삭제한다.
sample_incomplete_rows.drop("total_bedrooms",axis = 1)
#옵션2 "total_bedrooms"열에서 null이 있는지를 판단하는게 아니라 그냥 열자체를 삭제함
#axis = 0을 사용하면 행을 삭제함.
median = housing["total_bedrooms"].median()
sample_incomplete_rows["total_bedrooms"].fillna(median,inplace = True)
#옵션3 중간값으로 null값을 대처한다.
#fillna는 na를 찾으면 거기에 median 값을 대체해 넣는 함수다. inplace = false는 새로운 데이터프레임을 만들고 True는 기존 데이터 프레임에 덮어 넣는다.
sample_incomplete_rows이 중에 옵션3을 더 다뤄보자.
옵션3은 사이킷런의 SimpleImputer로 손쉽게 다룰 수있다.
중간값은 수치형 특성에서만 계산될 수 있기 때문에 텍스트 특성인 ocean_proximity를 제외하고 분석하기 위해 housing_num 복사본을 만든다.
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy ="median")
#mean(평균값으로), most_frequent(가장 많이 있었던 데이터로), constant(임의로 지정한값을 넣는다. fill_value 파라미터 사용)
housing_num = housing.drop("ocean_proximity",axis = 1)
imputer.fit(housing_num) #imputer의 fit메소드를 활용하여 housing_num 데이터를 imputer에 가동시킨다.
imputer.statistics_imputer는 각 특성의 중간값을 계산해서 그 결과를 객체의 statistics_속성에 저장한다.
imputer 매개변수중 뒤에 _가 있으면 imputer가 직접 생성한 값들로 구성된 파라미터라고 보면된다.
imputer.statistics와 housing_num.median().values와 비교해보면, 동일한 중앙값임을 알 수 있다.
구해진 median값을 housing_num데이터에 변환시켜주고, X 객체로 할당시키자.
그 이유는 사이킷런에 데이터를 가동하여 변환하면, 그 결과물은 numpy 배열로 나오기 때문에 이를 다시 pandas의 dataframe으로 변환시켜야한다.
X = imputer.transform(housing_num)
#구해진 median값을 housing_num 데이터에 변환시켜주는 imputer의 transform 메소드다.
housing_tr = pd.DataFrame(X, columns = housing_num.columns,
index = housing_num.index)
housing_tr잘 변형이 되었는지 확인해보자. total_bedrooms 레이블에 null값이 있었으니 total_bedrooms를 중점으로 확인해보자.
아래 이미지를 보면 잘 변형된 것을 확인할 수 있다.
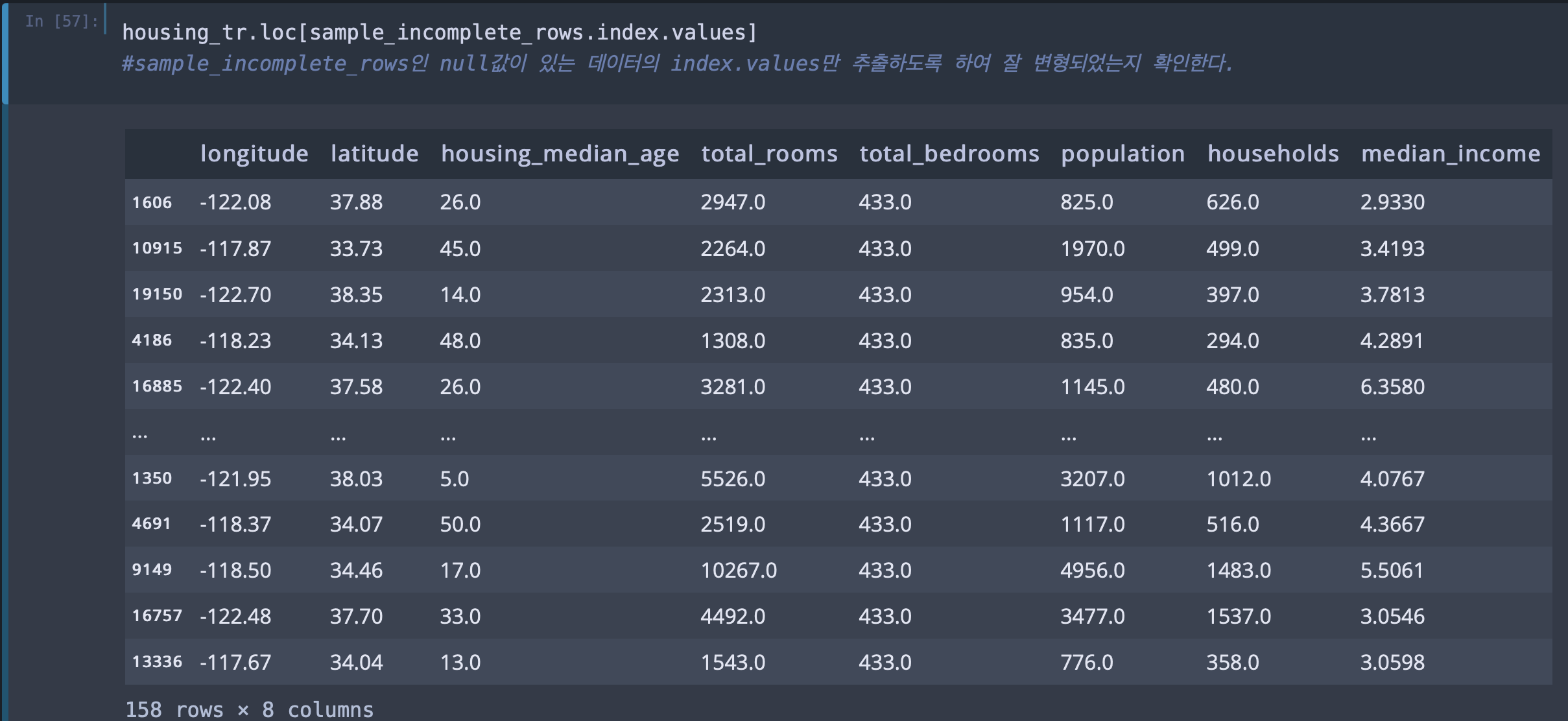
이제 범주형 데이터로 구성되어 있었던, ocean_proximity를 분석하기 수월하게 숫자형 데이터로 바꿔보자.
사이킷런에 OrdinalEncoder가 범주형, 문자형 데이터를 정수형 데이터로 바꿔준다.
from sklearn.preprocessing import OrdinalEncoder
ordinal_encoder = OrdinalEncoder()
housing_cat_encoded = ordinal_encoder.fit_transform(housing_cat) #fit과 Transform 메소드를 합한것. numpy배열로 나옴.
housing_cat_encoded[:10]
#문자열데이터가 숫자형 데이터로 변경되었음을 볼 수 있다.$ ordinal_encoder.categories_ 를 실행하면 숫자 배열이 어떻게 된건지 확인할 수 있다.
하지만, ordinal의 표현 방식의 문제는 머신러닝 알고리즘은 가까이 있는 두 값이 떨어져 있는 두 값보다 더 비슷하다고 생각하는 점이다. 예를 들어, ['bad','averge','good','excellent']와 같은 순서가 있는 카테고리 경우엔 상관없다. 그러나, 현재우리가 사용할 housing데이터의 ocean_proximity는 독립적인 범주형 데이터이므로 문제가 생긴다.
OneHotEncoder
위 문제점을 해결하기 위해 사이킷런의 OneHotEncoder를 사용한다.
OneHotEncoder는 하나의 특성만 1로 두고 다른 특성들을 다 0으로 두는 패키지다. 즉, 1H OCEAN을 1로 두면 나머지 특성은 다 0인 행렬로 구성된다는 것이다.
from sklearn.preprocessing import OneHotEncoder
cat_encoder = OneHotEncoder()
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hotonehotencoder은 1과 0으로 출력을 하므로 '희소 행렬'(각 행에 1이외에 대부분 0으로 채워져있는 행렬)이 된다.
이렇게 되면 0을 다 저장하기에는 메모리 낭비이므로 희소 행렬은 0이 아닌 원소의 위치만 저장한다.
일반적인 밀집 행렬(numpy행렬)로 바꾸려면 toarray()메서드를 호출하여 변형한다. 또는 처음부터 onehotencoder(sparse=False)를 사용한다.
housing_cat_1hot.toarray()
사이킷런이 유용한 변환기를 많이 제공하지만, 특별한 정제 작업이나 어떤 특성들을 조합하는 등의 작업을 위해 자신만의 변환기를 만들어야 할때가 있다. 내가 만든 변환기를 사이킷런의 기능과 매끄럽게 연동하고 싶을 때 아래와 같이 class를 만들어 신간과 노력을 전처리과정에서 줄일 수 있다.
fit와 transform을 만들어주고 transformerMixin을 상속하면 자동으로 fit_transform()를 생성하게 된다.
baseEstimator를 상속받으면 하이퍼파라미터 튜닝에 필요한 두 메서드(get_params와 set_params)를 추가로 얻게 된다.
from sklearn.base import BaseEstimator, TransformerMixin
#sklearn에서 계속 분석을 하고 있으면 되도록, sklearn에 있는 메서드로 분석 할 것. pandas갔다가 다시 sklearn썼다가 하면 통합이 어려움.
# 열 인덱스
rooms_ix, bedrooms_ix, population_ix, households_ix = 3, 4, 5, 6
class CombinedAttributesAdder(BaseEstimator, TransformerMixin): #BaseEstimator, TransformetMixin을 상속 받음.
def __init__(self, add_bedrooms_per_room=True): # *args 또는 **kargs 없음.
self.add_bedrooms_per_room = add_bedrooms_per_room
def fit(self, X, y=None): #여기서 X는 null값이 모두 median값으로 변형된 데이터 세트다.
return self # 아무것도 하지 않습니다
def transform(self, X):
rooms_per_household = X[:, rooms_ix] / X[:, households_ix]
population_per_household = X[:, population_ix] / X[:, households_ix]
if self.add_bedrooms_per_room:
bedrooms_per_room = X[:, bedrooms_ix] / X[:, rooms_ix]
return np.c_[X, rooms_per_household, population_per_household,
bedrooms_per_room]
else:
return np.c_[X, rooms_per_household, population_per_household]
attr_adder = CombinedAttributesAdder(add_bedrooms_per_room=False)
housing_extra_attribs = attr_adder.transform(housing.to_numpy())위 class를 통해 추가로 직접만든 특성들을 추가시켜보았다.
$ housing_extra_attribs를 실행하면, numpy 배열로 나온다. 그러므로, pd.DataFrame으로 dataframe을 만들어주자.
housing_extra_attribs = pd.DataFrame(
housing_extra_attribs,
columns = list(housing.columns)+["rooms_per_household","population_per_household"],
index = housing.index)
housing_extra_attribs.head()
이제 pipeline을 활용해, 데이터 사전 처리 및 분류의 모든 단계를 포함하는 단일 개체를 만들어보자.
그리고, 데이터 스케일 조정이 필요할 때 사용할 수 있는 StandardScaler를 불러와서 활용하자.
pipeline은 리스트로 변환기들을 입력할 수 있다. 그 리스트안에 있는 요소들은 튜플로 이름과 클래스 객체로 넣는다. 교차검증을 하려면 pipeline을 사용하는게 좋다.
StandardScaler는 평균 0, 분산 1(표준편차 1)로 조정한다. fit, transform, fit_transform을 다 지원한다.
from sklearn.pipeline import Pipeline #수치형 특성을 전처리 하는 pipeline을 불러옴.
from sklearn.preprocessing import StandardScaler
num_pipeline = Pipeline([
('imputer',SimpleImputer(strategy = "median")), #null값을 Median으로 대처
('attribs_adder', CombinedAttributesAdder()), #추가시킬 레이블 추가.
('std_scaler',StandardScaler()),#수치형 특성을 표준 정수로 바꾸기 위한 것. 즉 표준화 시키는 것.
])
#이 세개를 pipeline에 통합을 하여,
housing_num_tr = num_pipeline.fit_transform(housing_num) #pipeline 자체를 변환기처럼 사용할 수 있다.$ housing_num_tr 이렇게 실행을 하면 누락된 값도 median으로 대처가 되고,(SimpleImputer)
더 첨가하고 싶었던 특성들도 첨가할 수 있게 되고,(CombinedAttributesAdder), 표준화된 수치들로 구성되었다.
수치형 데이터는 pipeline을 통해 한번에 변형시킬 수 있는 객체를 만들었고, 이제 범주형 데이터를 변형시켰던 OneHotEncoder도 함께 묶어서 ColumnTransformer를 통해 full_pipeline을 만들어보자.
from sklearn.compose import ColumnTransformer #ColumnTransformer은 각열마다 다른 변환기를 적용할 수 있는 도구
#CilumnTransformer 클래스는 튜플의 리스트를 받고 각 튜플은 이름, 변환기, 변환기가 적용될 열 이름의 리스트로 이루어진다.
num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
full_pipeline = ColumnTransformer([
("num",num_pipeline,num_attribs), #num_attribs는 num_pipeline인 변환기를 적용한다. num_pipeline은 밀집 행렬을 반환한다.
("cat",OneHotEncoder(), cat_attribs), #cat_attribs는 OneHotEncoder인 변환기를 적용한다. OneHotEncoder은 희소 행렬을 반환한다.
])
#ColumnTransformer은 최종 행렬의 밀집 정도(즉 0이 아닌 원소의 비율)를 추정한다.밀집도가 임곗값(기본적으로 sparse_threshold=0.3)보다 낮으면 희소, 높으면 밀집이 반환된다.
housing_prepared = full_pipeline.fit_transform(housing)
full_pipeline$housing_prepared.shape는 데이터 세트의 행렬 크기를 알려준다.
16512는 기존 train 세트와 동일하게 행의 갯수가 같고 16은 수치형 데이터 세트(num_attribs)에서의 8개와 새롭게 추가시켰던 속성(CombinedAttributesAdder변환기로 추가 시킨) 3개와 범주형 데이터를 5개로 나눴던 (OneHotEncoder 변환기로 나눈) 5개 열까지 해서 16가지의 열을 생성하여 만들어졌다.
LinearRegression
지금까지 데이터를 수집하고 살펴보고 모델링하기 좋게 전처리까지 했다. 지금부터는 모델을 선택하고 훈련을 할 것이다.
우선 회귀분석먼저 해보자.
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)
some_data = housing.iloc[:5]
#housing data 는 현재 실제 집값 열만 drop하고 남은 데이터 세트다.
some_labels = housing_labels.iloc[:5]
#housing_labels는 실제 집값 열인 데이터 세트다.
some_data_prepared = full_pipeline.transform(some_data)
#housing 데이터를 full_pipeline에 넣어서 작동 시켰다. full pipeline은 ColumnTransformer의 변환기로 각열마다 각 다른 변환기를 사용하는것.
print("예측:",lin_reg.predict(some_data_prepared))
print("레이블:",list(some_labels))
housing 데이터에서 5개 행, housing_labels 데이터에서 5개 행만 가져와서 linearregression을 돌려본 결과, 아래 같이 나왔다.
예측과 실제 레이블 값과 비교하면, 정확한 예측은 아니지만, 작동은 한다.

예측률들을 계산하여 비교해보자.
for i in range(5):
print(list(some_labels)[i] / list(lin_reg.predict(some_data_prepared))[i] *100)
회귀분석에서 전형적으로 사용하는 성능 지표인 평균 제곱근 오차(RMSE)를 구해보자.
from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels,housing_predictions)
lin_rmse = np.sqrt(lin_mse)
lin_rmse결과는 아래 값으로 나온다. 중간 주택 가격이 120,000 부터 265,000 사이임을 감안하면, RMSE값이 68627은 매우 만족스럽지 못하다.
68627.87390018745이런 상황은 특성들이 좋은 예측을 만들 만큼 충분한 정보를 제공하지 못했거나 모델이 충분히 강력하지 못하다는 사실을 말해준다.
과소적합을 해결하는 주요 방법은 세가지가 있다. 우선 우린 1번을 선택하여 진행해보자.
1.더 강력한 모델을 선택하거나
2.훈련 알고리즘에 더 좋은 특성을 주입하거나
3.모델의 규제를 감소시키는 것이다.
DecisionTreeRegressor
DecisionTreeRegressor 모델을 택하여 진행해봤다.
from sklearn.tree import DecisionTreeRegressor
#DecisionTreeRegressor인 결정트리는 강력하고 데이터에서 복잡한 비선형 관계를 찾을 수 있다.
tree_reg = DecisionTreeRegressor()
tree_reg.fit(housing_prepared,housing_labels)
housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse결과는 0.0 이 나왔다. 결과가 0인 것을 보아, 과대적합을 의심해 볼 필요가 있다. 테스트세트는 되도록 건들지 않는 것이 좋기 때문에, 교차 검증을 통해 훈련데이터와 검증데이터를 나누어 모델의 성능을 확인해보자.
교차검증
교차 검증으로는 사이킷런의 <k-겹 교차 검증> 기능을 사용하는 방법이 있다.
아래 코드는 훈련 세트를 폴드라 불리는 10개의 서브셋으로 무작위로 분할한다. 그런 다음 결정 트티 모델을 10번 훈련하고 평가한다.
매번 다른 폴드를 선택해 평가에 사용하고 나머지 9개 폴드는 훈련에 사용한다. 이렇게 10번 훈련을 시켜서 10개의 평가 점수가 담긴 배열이 결과가 된다.
from sklearn.model_selection import cross_val_score
scores = cross_val_score(tree_reg, housing_prepared, housing_labels,
scoring = "neg_mean_squared_error",cv = 10)
tree_rmse_scores = np.sqrt(-scores)
tree_rmse_scores사이킷런의 교차 검증은 scoring 매개변수에 (낮을수록좋은)비용함수가 아니라 (클수록좋은)효용함수를 기대한다. 그래서 평균제곱오차(MSE)의 반댓값(즉,음수값)을 계산하는 neg_mean_squared_error함수를 사용한다.이런 이유로 scores에 -를 붙인 것이다.
rmse 값이 10개 나왔을 것이므로, 10개의 값들의 평균과 표준편차를 확인해보자.
def display_scores(scores):
print("점수:",scores)
print("평균:",scores.mean())
print("표준편차:",scores.std())
display_scores(tree_rmse_scores)
결과는 썩 좋지 않다. 위에서 분석했던 선형회귀보다 안좋다.
선형회귀도 교차검증을 사용해서 평가해보자.
lin_scores = cross_val_score(lin_reg,housing_prepared,housing_labels,
scoring = "neg_mean_squared_error",cv = 10)
lin_rmse_scores = np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)
선형회귀 결과보다 결정트리 결과가 나쁜것을 보여 확실히 결정 트리 모델이 과대적합되어 선형 회귀 모델보다 성능이 나쁘다고 생각할 수 있다.
RandomForestRegressor
마지막으로 RandomForestRegressor 모델을 하나 더 시도 해보자.
RandomForestRegressor모델은 특성을 무작위로 선택해서 많은 결정 트리를 만들고 그 예측을 평균 내는 방식이다.
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor()
forest_reg.fit(housing_prepared, housing_labels)
forest_reg
#성능 계산
housing_predictions = forest_reg.predict(housing_prepared)
forest_mse = mean_squared_error(housing_labels,housing_predictions)
forest_rmse = np.sqrt(forest_mse)
forest_rmse18731.191395437647 값이 나온다. 뭔가 느낌이 좋은 rmse값이다.
교차검증도 해보자.
forest_scores = cross_val_score(forest_reg,housing_prepared,housing_labels,
scoring = "neg_mean_squared_error",cv = 10)
forest_rmse_scores = np.sqrt(-forest_scores)
forest_rmse_scores
display_scores(forest_rmse_scores)
하지만, 훈련세트에 대한 점수(forest_rmse)가 검증세트에 대한 점수(forest_rmse_scores)보다 훨씬 낮으므로 이 모델도 여전히 훈련세트에 과대적합되었다. 과대적합을 해결하기 위해서는 1.모델을 간단히한다., 2.제한을 한다.,3.더 많은 훈련 데이터를 모은다.를 해야한다.
이제 어느정도, 적합한 모델을 찾았다고 본다. RandomForestRegressor에서 과대적합이 있는것으로 보이니, 이에 적합한 하이퍼파라미터를 잡고 이 모델에 맞는 제한을 주자.
그리드 탐색(gridsearch) & 랜덤 탐색 이론
그리드 탐색은 데이터 준비 단계를 하나의 하이퍼파라미터처럼 다룰 수 있다. 예를 들면 그리드 탐색이 확실하지 않은 특성을 추가할지 말지 자동으로 정할 수 있다.
비슷하게 이상치나 값이 빈 특성을 다루거나 특성 선택 등을 자동으로 처리하는 데 그리드 탐색을 사용한다.
그리드 탐색은 내가 입력한 하이퍼파라미터를 순차적으로 일일히 다 테스트하여 평가하는 것이다. 단점으로는 시간이 너무 많이 걸린다.
랜덤 탐색은 하이퍼파라미터 탐색 공간이 커지면 사용하는 편이 좋다. RandomizedSearchCV는 GridSearchCV와 거의 같은 방식으로 사용하지만 가능한 모든 조합을 시도하는 대신 각 반복마다 하이퍼파라미터에 임의의 수(랜덤)를 대입하여 지정한 횟수만큼 평가한다.
트리 모델의 앙상블이 랜덤 포레스트다.
GridSeachCV는 탐색하고자 하는 하이퍼파라미터와 시도해볼 값을 지정하면 가능한 모든 하이퍼파라미터 조합에 대해 교차 검증을 사용해 평가하게 된다.
from sklearn.model_selection import GridSearchCV
param_grid = [
{'n_estimators' : [3,10,30],'max_features':[2,4,6,8]},
{'bootstrap':[False],'n_estimators':[3,10],'max_features':[2,3,4]}
]
forest_reg = RandomForestRegressor()
#RandomForest 모델로 평가해보았다.
grid_search = GridSearchCV(forest_reg,param_grid,cv=5,
scoring = 'neg_mean_squared_error',
return_train_score = True)
grid_search.fit(housing_prepared, housing_labels)param_grid에서 첫번째 dict에 있는 n_estimators와 max_features 하이퍼파라미터의 조합인 3X4=12개를 평가하고
두번째 dict에 있는 n_estimators와 max_features 하이퍼파라미터의 조합인 2X3=6개를 평가해서, 12 + 6 = 18개 조합을 탑색한다.
(어떤 하이퍼파라미터 값을 지정해야 할지 모를 때는 연속된 10의 거듭제곱 수로 시도해보는 것도 좋다.)
각 다섯번 모델을 훈련시킨다.(5-겹 교차 검증을 사용하기 때문에) 다시 말해 전체 훈련 횟수는 18X5=90이 된다.
이제 18가지 유형의 각 하이퍼파라미터로 각각 분석한 성과 지표는 어떻게 될지 확인해보자.
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score),params)
위 결과를 보면, 이 예에서는 max_features 하이퍼파라미터가 6, n_estimators 하이퍼파라미터가 30일 떼 최적의 솔루션이다.
이때, RMSE 점수가 49,957으로 앞서 기본 하이퍼파라미터 설정으로 얻은 50379점 보다 조금 더 좋다.
성공적으로 최적의 모델을 찾았다.
이제 각 특성중에 어떤 특성이 가장 중요하고 의미있는지 확인해보자. 즉, 특성별 중요도를 탐색해보자는 것이다. 이것은 트리모델이라 가능한 것이다.
extra_attribs= ["rooms_per_hhold","pop_her_hhold","bedrooms_per_room"] #따로 만들었던 extra 특성들을 따로 추가시키기위해 리스트형태로 묶는다.
cat_encoder = full_pipeline.named_transformers_["cat"] #pipeline에서 ocean_proximity를 OnHotIncoding한 것을 cat으로 이름을 정했었는데, 이부분만 따로 빼온다.
cat_one_hot_attribs = list(cat_encoder.categories_[0]) #cat_encoder에서 categories값만 뽑는다.categories는 np-array이므로 [0]로 1행만 리스트로 빼낸다.
attributes = num_attribs + extra_attribs +cat_one_hot_attribs #그리고 순서에 맞게 합친다.
sorted(zip(feature_importances,attributes),reverse = True) #zip함수를 활용해서 featur_importances값과 attributes를 합친다. 역순으로.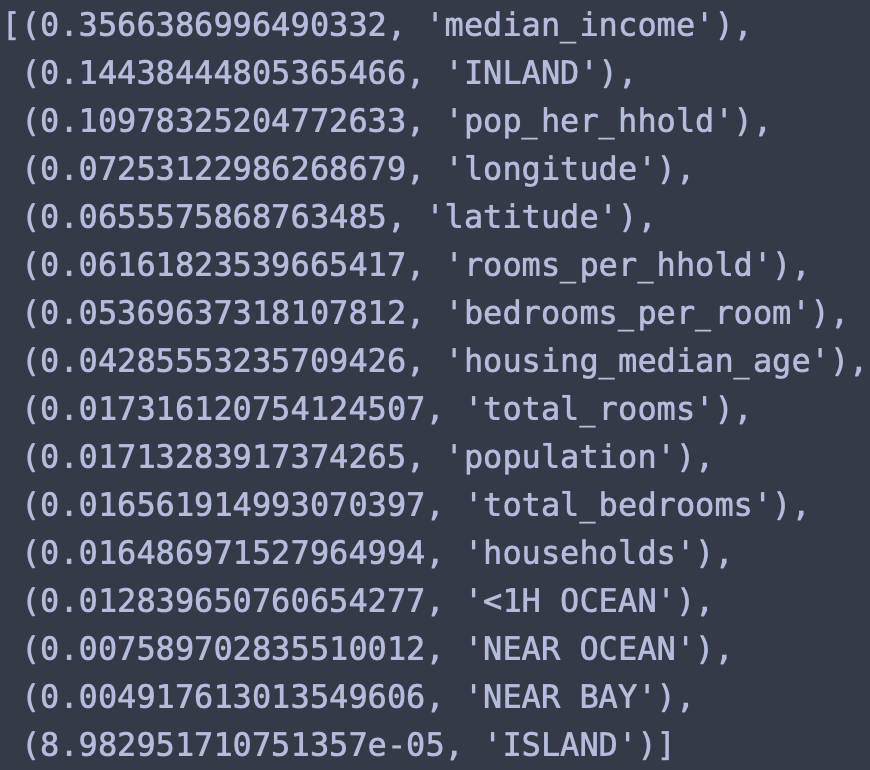
결과를 보면 median_income이 가장 성과내는데 도움을 줬고 의외로 범주형특성인 inland가 유용한 특성으로 나왔다. pop_her_hhold도 유용하다고 나온다.
test_data로 평가
가장 성능이 좋았던 grid_search.best_estimator_를 fimal_model로 지정하고 test데이터를 가져와 평가해보자.
final_model = grid_search.best_estimator_
#test데이터에서 X와 y를 나누어 X에는 median_house_value를 제거하고 y에는 median_house_value만 복사한다.
X_test = strat_test_set.drop("median_house_value",axis = 1)
y_test = strat_test_set["median_house_value"].copy()
#X_test에 full_pipeline을 활용하여 변환시킨다.
X_test_prepared = full_pipeline.transform(X_test)
#그후, final_model로 분석을 해본다.
final_predictions = final_model.predict(X_test_prepared)
#분석한, 결과는 mse와 rmse로 평가한다.
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
나쁘지 않다. 만족스럽다.
이 추정값이 얼마나 정확한 지를 알기 위해 scipy.stats.t.interval()를 사용해 일반화 오차의 95% 신뢰 구간을 계산할 것이다.
from scipy import stats
confidence = 0.95 #신뢰구간
squared_errors = (final_predictions - y_test) ** 2 #모든 샘플에 대한 제곱오차다. 신기한 건, final_prediction은 넘파이 배열이고 y_test는 series객체인데, 둘을 빼면 series객체로 나온다.
np.sqrt(stats.t.interval(confidence, len(squared_errors)-1, #자유도 1로 두고 샘플에서 1을 뺀다.
loc = squared_errors.mean(),
scale = stats.sem(squared_errors))) #표준오차, squared_error.sem()으로도 사용 가능.
신뢰구간은 45798부터 49655까지가 95% 신뢰구간임을 알 수 있고, 모평균값이 이 구간에 있을 확률이 95%라는 말이다.
마무리
다양한 프로젝트도 학교에서 해봤지만, 부족한 분석기술로 진행해 왔구나를 깨달았다. 이번 프로젝트를 공부하면서, 다양한 전처리 기술과 분석기술 pipeline활용, 그리드 탐색, sklearn 활용등을 배우면서 꼭 다음 공모전에 참가하면, 이런 기술들로 더 나은 성과를 낼 수 있도록 해야겠다고 다짐했다. 그래서 더 꼼꼼히 공부하고 기록했던거같다.